Nov 23, 2021 11 min read cryptography

OverTheWire Krypton (Levels 0-9)

OverTheWire is an educational hacking site with different “war games” meant to teach different topics (for example, Natas teaches web security).

Krypton is a short war game focused on introductory cryptography concepts.

Level 0 ➔ 1

Head over to OverTheWire’s Krypton page to see the first level’s information:

We’re instructed to SSH into the server with username krypton1, hostname krypton.labs.overthewire.org and port 2231. To do so, open up a terminal window and type the follow (where the $ is the prompt symbol and does not need to be added in by you):

$ ssh krypton1@krypton.labs.overthewire.org -p 2231

The instructions tell us that the password is Base64 encoded, so we’ll need to Base64 decode it. I prefer to use CyberChef for quick CTF calculations:

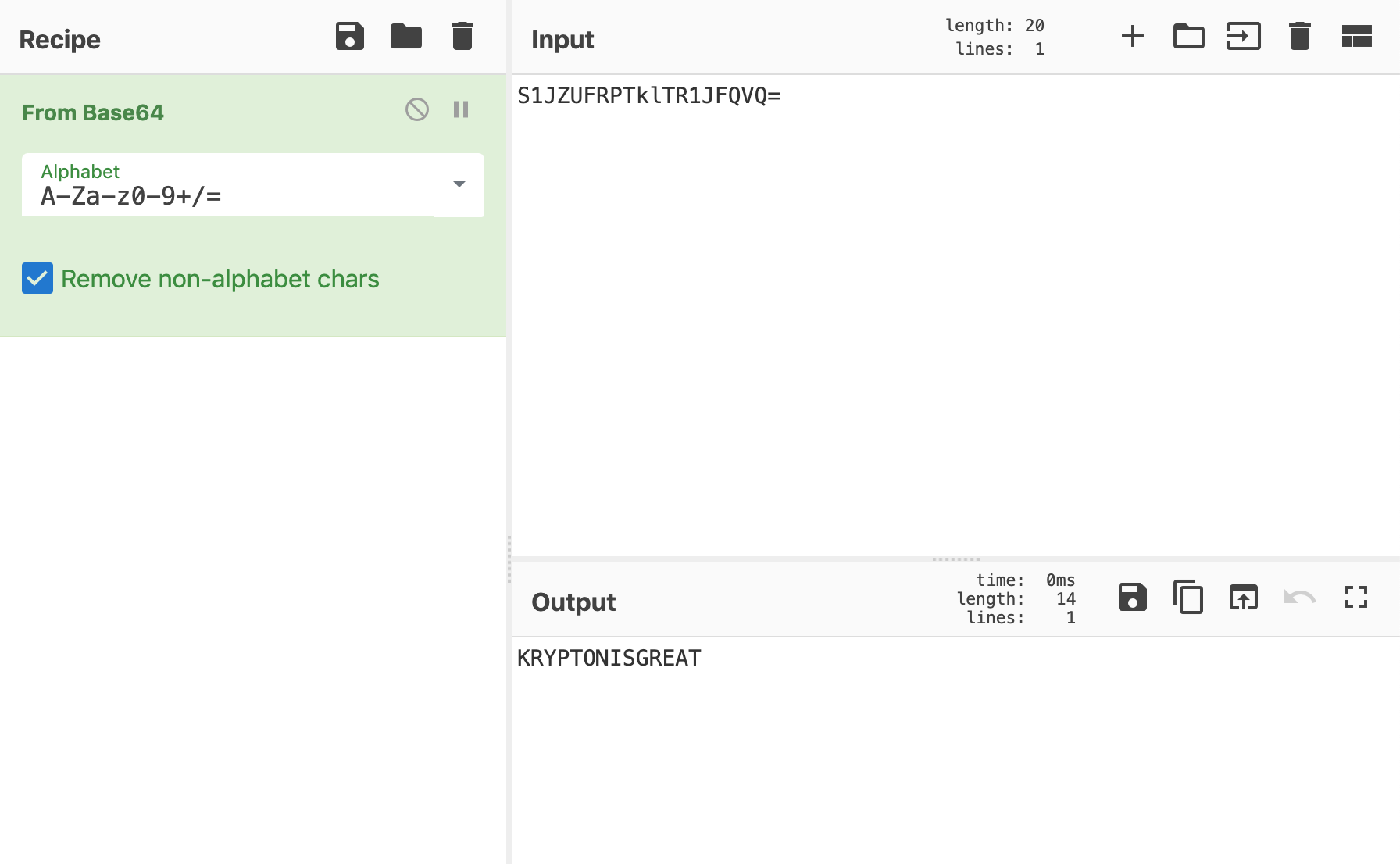
We see that the password is KRYPTONISGREAT.

Enter that when prompted, and we’re logged in!

Level 1 ➔ 2

The rest of the welcome message says that Most LEVELS are stored in /somegame/. That means we should change directory (cd) to /krypton:

From there, we’ll need to cd into krypton1, and read the README:

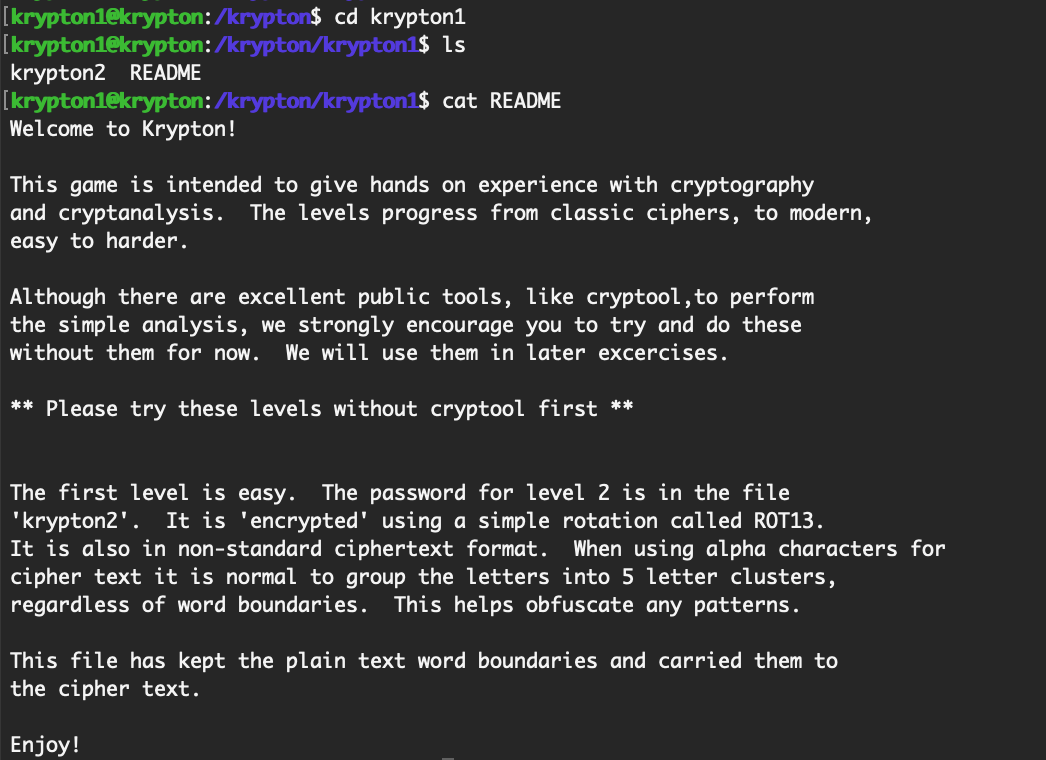
The instructions spell out that it’s a ROT13 cipher. ROT13 is a variation of a Caesar Cipher, which is a simple monoalphabetic substitution cipher. This means that each letter is substituted using the same alphabet shift (in this case, 13).

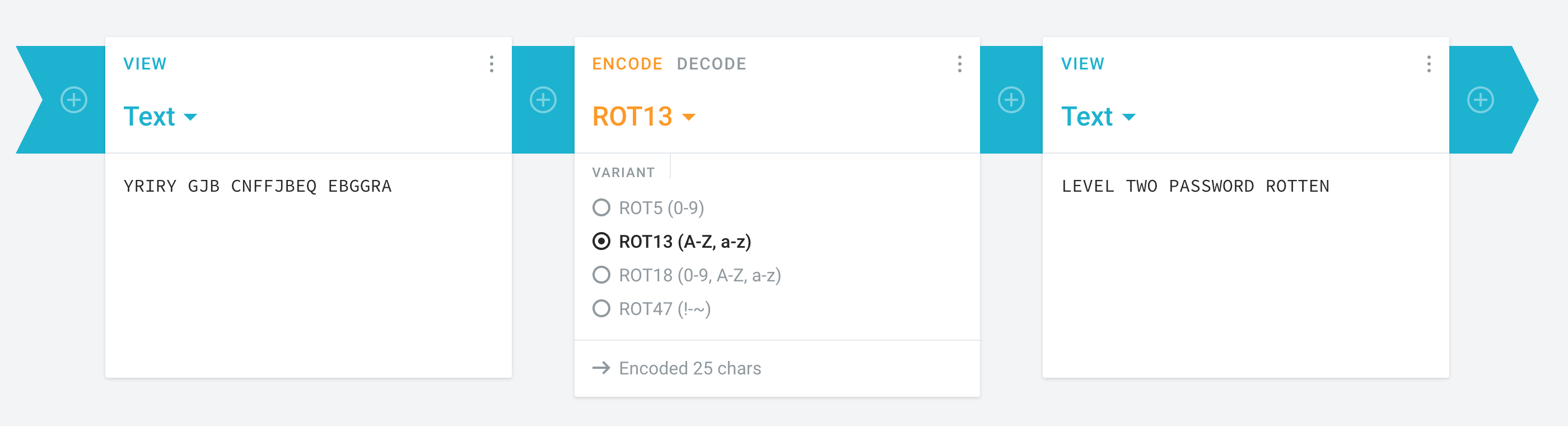
To test this out yourself, use a site like Cryptii. Select the cipher method (ROT13) from the dropdown, and get the password for the next level (ROTTEN):

Level 2 ➔ 3

Exit the previous SSH session, and begin a new one as the user for the next Krypton level, krypton2:

ssh krypton2@krypton.labs.overthewire.org -p 2231

We’ll have to cd to the challenge directory again:

cd /krypton/krypton2

Let’s have a look at the README file:

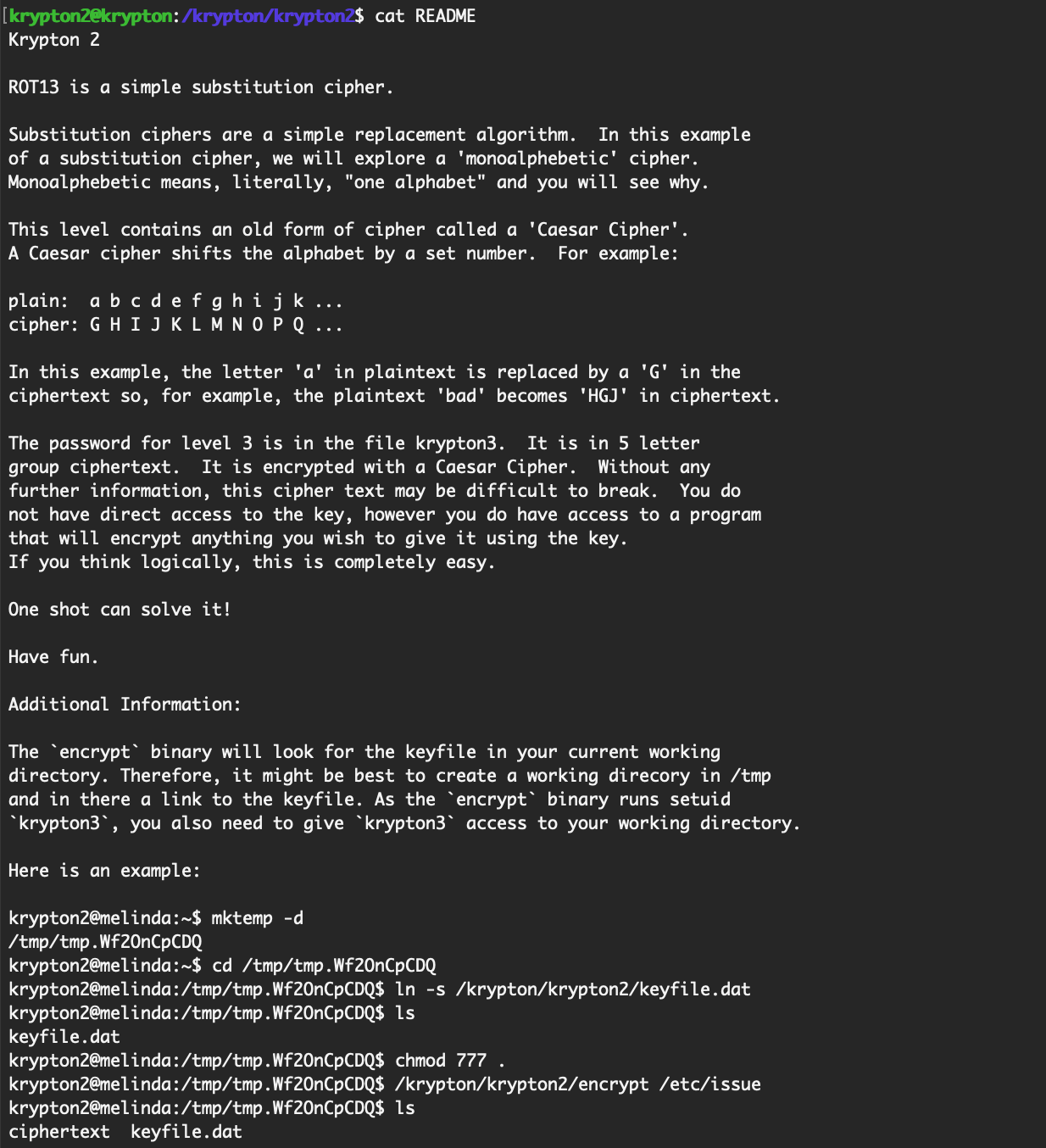
In short, we have an encrypted key file, and a program that will encrypt our input using the same method.

We also know that it’s a Caesar Cipher (traditionally a shift of 3, where ROT13 is a shift of 13), but we need to find the exact shift value.

We can either brute force the encrypted key file, as there are only 25 different possible shifts (one for each letter of the alphabet, minus the one that maps back to the same letter), or we can try to encrypt our own information.

If we take the latter approach, let’s follow the instructions given to make a temporary folder and make a symbolic link of keyfile.dat:

krypton2@krypton:/tmp$ mktemp -d
/tmp/tmp.1mLghTok9p
krypton2@krypton:/tmp$ cd /tmp/tmp.1mLghTok9p
krypton2@krypton:/tmp/tmp.1mLghTok9p$ ln -s /krypton/krypton2/keyfile.dat
krypton2@krypton:/tmp/tmp.1mLghTok9p$ ls
keyfile.dat
krypton2@krypton:/tmp/tmp.1mLghTok9p$ chmod 777 .

Next, let’s make a test file containing the letter “A”:

echo "AAA" > example.txt

Once we encrypt the file, it will be shifted to a different letter. The difference between this letter and A will be the Caesar cipher shift value:

The value is M, meaning that we have a shift of 12 (from A to M, the 12th letter of the alphabet) to encode. To decode, we can use a tool like cryptii again, or shift the letters of OMQEMDUEQMEK 12 backwards, or 14 forwards (since 26 letters – 12 = 14) to wrap back around.

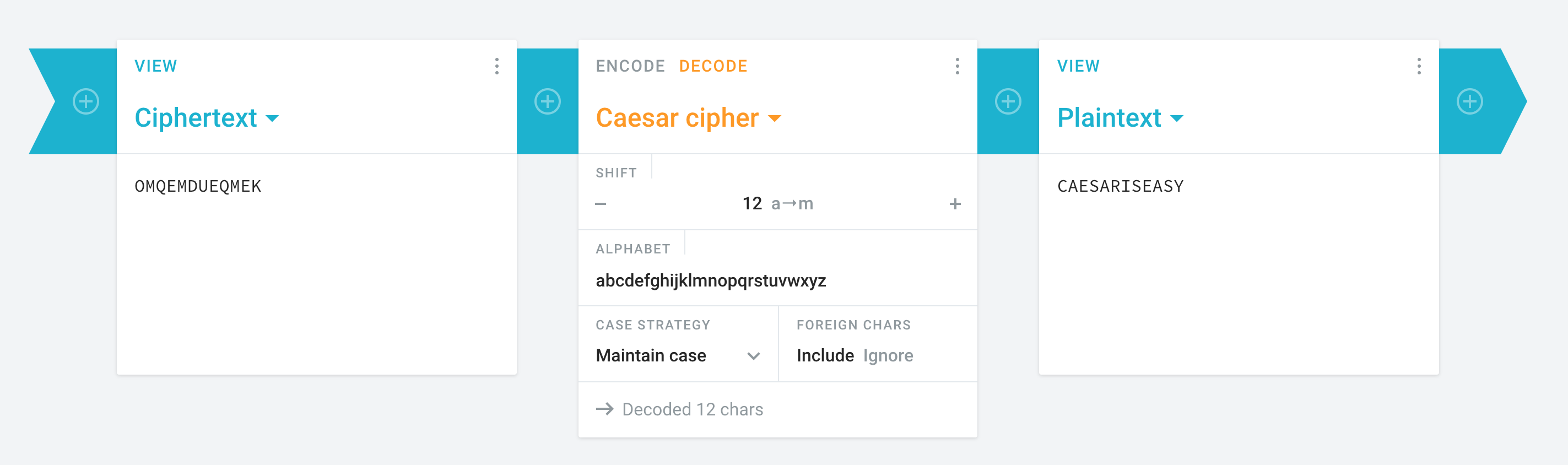
Our flag for the next level is CAESARISEASY.

Level 3 ➔ 4

ssh krypton3@krypton.labs.overthewire.org -p 2231

We’ll need to cd to the challenge directory:

The READMEtells us that we’ve moved past a simple substitution cipher, but we’re lucky that multiple ciphertexts have been intercepted.

If we look at the available ciphertexts (found1, found2, etc), we notice that they’re all in a similar format of 5 letters separated by spaces. But we don’t know if that’s because of the cipher used, or a way of obfuscating any patterns.

The README says that the original texts are in English. Why does this matter? It’s likely a hint that we need to use frequency analysis to find the key.

We can use a tool like this one to map out the frequency of letters in our cipher texts against typical frequency of letters in English texts:

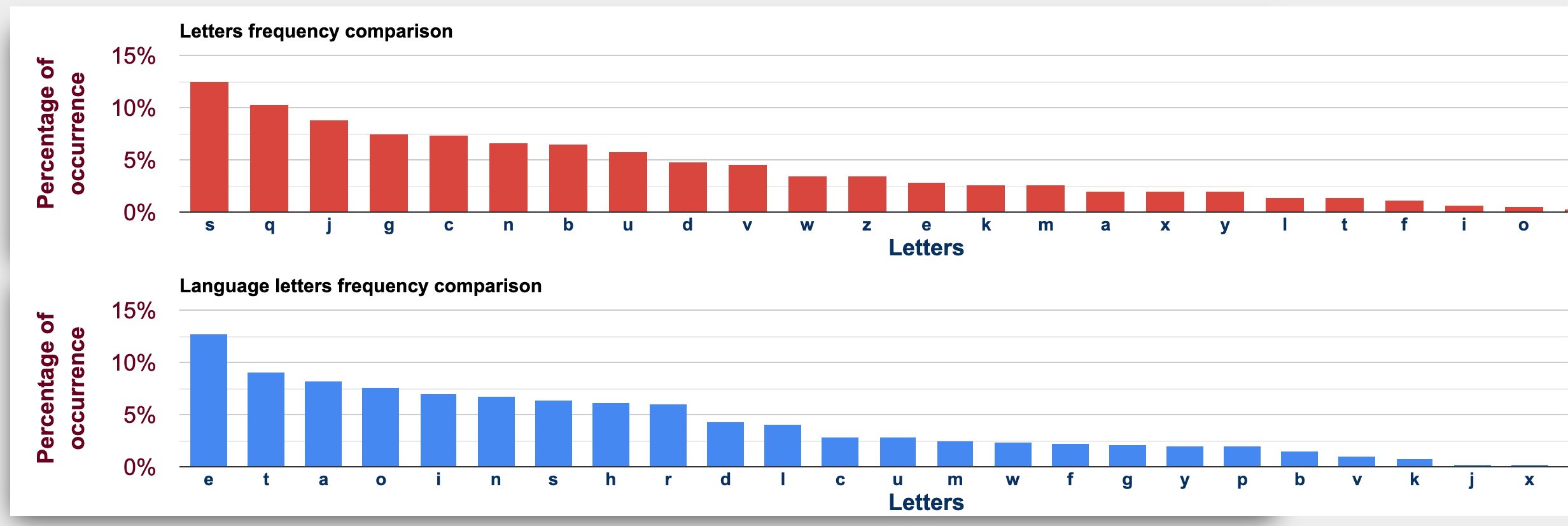
From this we can see that the letter S in our ciphertext likely maps to e in plaintext, Q to t, and so on.

We can also use tools like this one to find that JDS is the most common three letter trigraph in the text, and likely maps to a common English three-letter word like the or and.

If that’s the case, the frequency graph shown above can’t be taken at face value. Rather than J mapping to A, for example, it could map to T (if jds -> the), meaning the second and third bars in the graph are out of order.

One more hint that we have is that there are repeating letters in the encrypted flag:

KSVVW BGSJD SVSIS VXBMN YQUUK BNWCU ANMJS

VV maps to the same letter twice, and UU map to another repeated letter later on in the text. Only certain letters in the English language are repeated (e.g. S, T, E) which helps narrow our choices down further.

The longer the text, the more accurate the frequency analysis will be. If we were solving using only the flag cipher text, our analysis would be less accurate and more guess-y.

From here, you have two options. First, you can use a tool such as this one to individually swap out letters as you make educated guesses:

Or you can use a tool like quipquip which will solve it for you. To do so, take one of the longer ciphertexts and paste it into the site, then add the password to the end of the ciphertext.

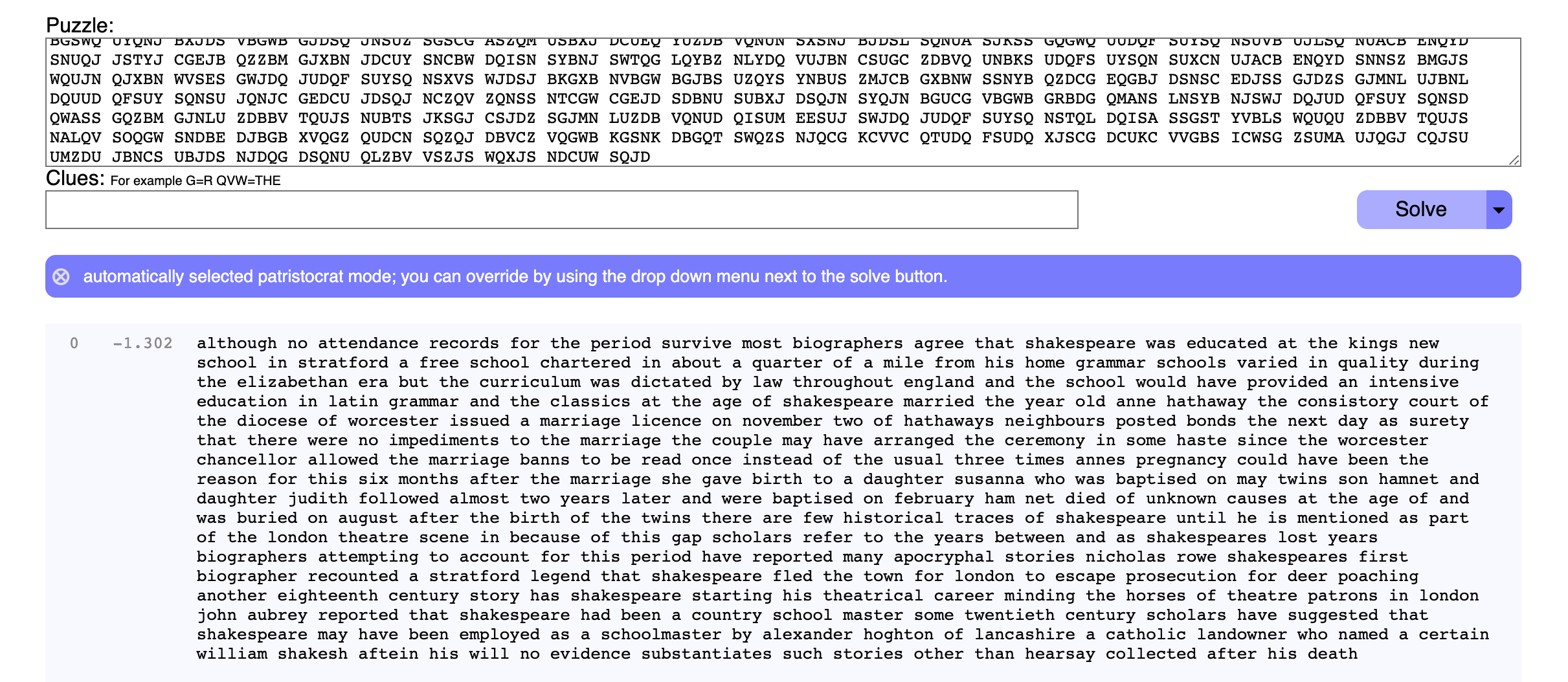
Then click solve:

The password is actually going to be uppercase (“BRUTE”), the tool converts the output to lowercase to help differentiate between input and output.

Level 4 ➔ 5

SSH into the site with ssh krypton4@krypton.labs.overthewire.org -p 2231 and password BRUTE. Then cd into /krypton/krypton4.

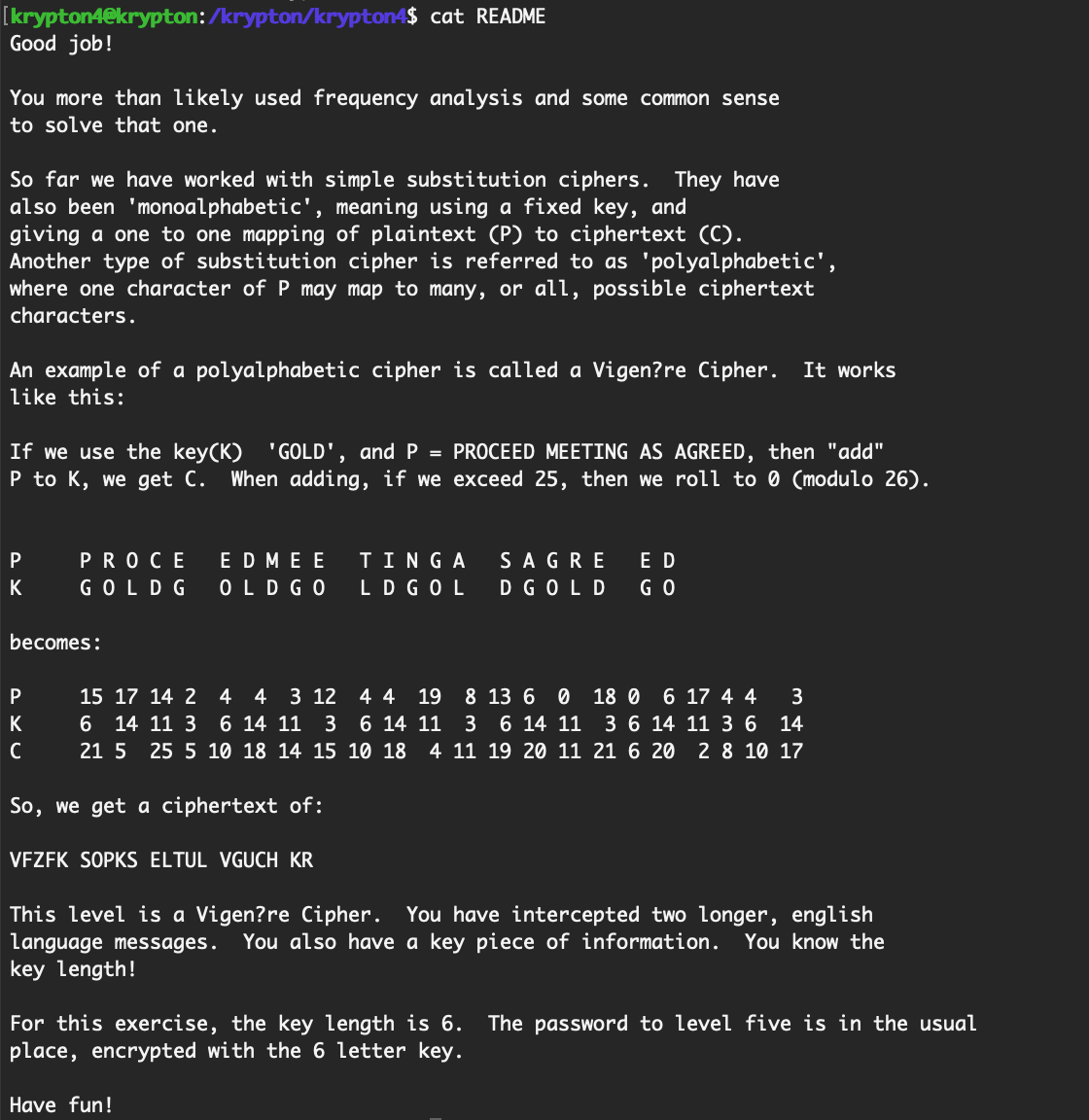
The README tells us some interesting info, namely that:

This level uses a Vigenère cipher, and
The key length is 6

Vigenère is like an upgraded version of the Caesar cipher. Rather than each letter being shifted by the same amount, there’s a key that encodes letter 1 to a certain shift, letter 2 to another shift, and so on.

After 6 letters (the key length), the pattern repeats, so knowing the key length will help us solve it.

The flag cipher text is very short: HCIKV RJOX.

Much like the previous level, the longer the cipher text is, the more accurate our analysis will be. So, we’ll need to use the two found cipher texts to determine the key.

Using a tool like Dcode.fr, copy/paste the text from found1 into the website. Type in 6 for the key length:

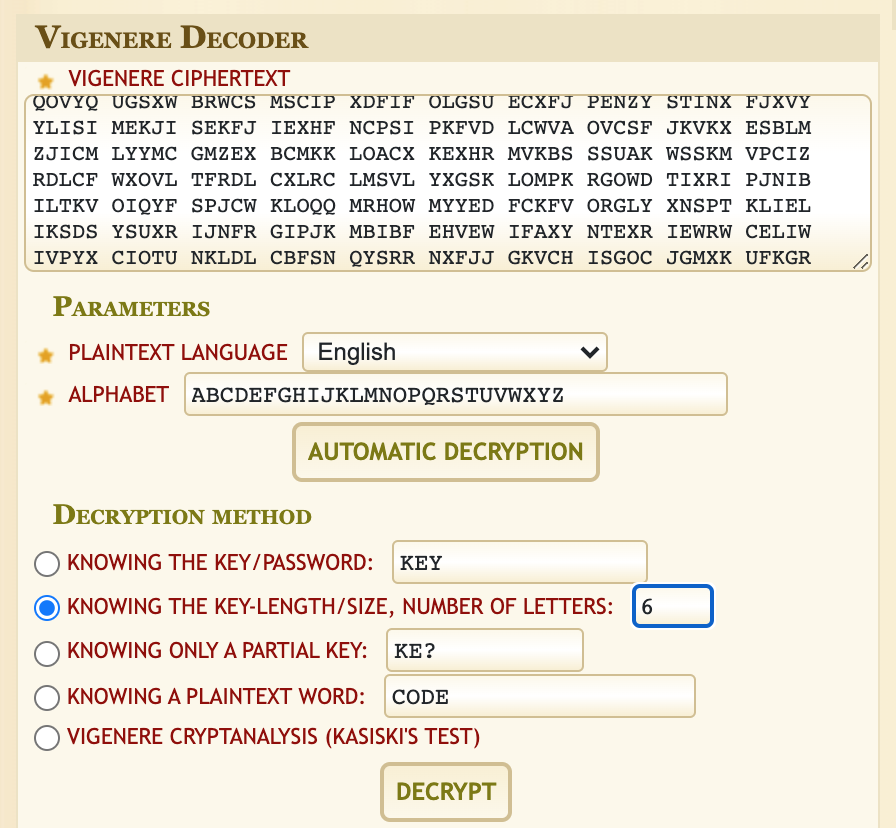
Hit Decrypt and it will show the best guess at the key. The first key of FREKEY seems to have correct, readable text:

Open up another tab and provide FREKEY as the key, then hit Decrypt. The result (and flag for the next level) is CLEARTEXT.

Level 5 ➔ 6

SSH in with ssh krypton5@krypton.labs.overthewire.org -p 2231 and password CLEARTEXT.

The README this time says no key length will be provided. Our first goal then will be to figure out the key length, then use that to find the key (and make analysis easier on the tools we’re using).

However, if we go back to Dcode.fr, enter in the text from found1 and hit Automatic Decryption, it does both steps instantly for us.

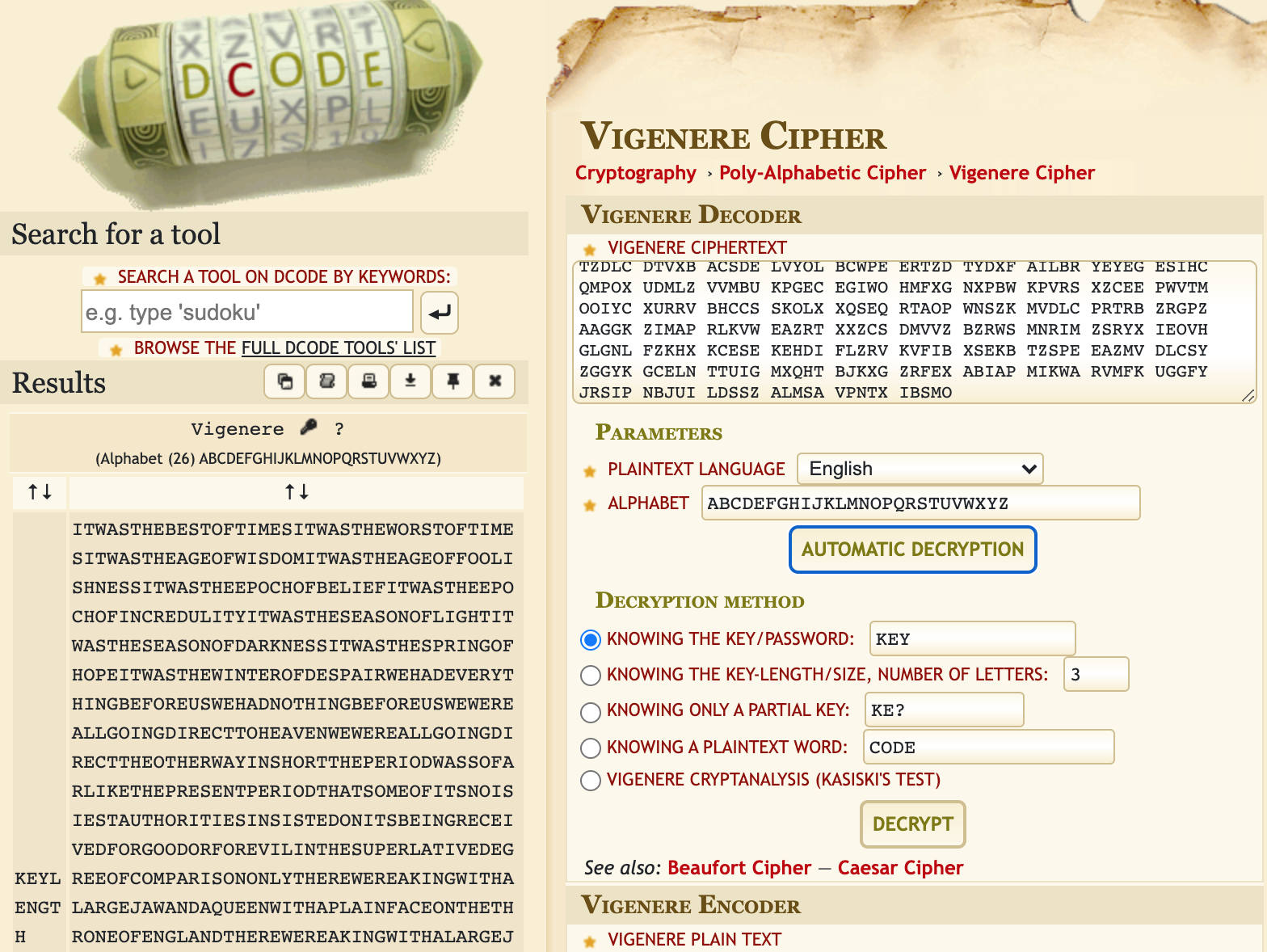
The key is KEYLENGTH. If we use that to decrypt the ciphertext of BELOS Z, we get RANDOM.

Level 6 ➔ 7

The README is pretty long this time, explaining why randomness in cryptography is important, how one-time pads work, and a very brief introductory to modern ciphers:

$ cat README
Hopefully by now its obvious that encryption using repeating keys is a bad idea. Frequency analysis can destroy repeating/fixed key substitution crypto.

A feature of good crypto is random ciphertext. A good cipher must not reveal any clues about the plaintext. Since natural language 
plaintext (in this case, English) contains patterns, it is left up to the encryption key or the encryption algorithm to add the 'randomness'.

Modern ciphers are similar to older plain substitution ciphers, but improve the 'random' nature of the key.

An example of an older cipher using a complex, random, large key is a vigniere using a key of the same size of the plaintext. For
example, imagine you and your confident have agreed on a key using the book 'A Tale of Two Cities' as your key, in 256 byte blocks.

The cipher works as such:

Each plaintext message is broken into 256 byte blocks. For each block of plaintext, a corresponding 256 byte block from the book
is used as the key, starting from the first chapter, and progressing. No part of the book is ever re-used as key. The use of a key of the same length as the plaintext, and only using it once is called a "One Time Pad".

Look in the krypton6/onetime directory. You will find a file called 'plain1', a 256 byte block. You will also see a file 'key1', the first 256 bytes of 'A Tale of Two Cities'. The file 'cipher1' is the cipher text of plain1. As you can see (and try) it is very difficult to break
the cipher without the key knowledge.

(NOTE - it is possible though. Using plain language as a one time pad key has a weakness. As a secondary challenge, open README in that directory)

If the encryption is truly random letters, and only used once, then it is impossible to break. A truly random "One Time Pad" key cannot be broken. Consider intercepting a ciphertext message of 1000 bytes. One could brute force for the key, but due to the random key nature, you would produce every single valid 1000 letter plaintext as well. Who is to know which is the real plaintext?!?

Choosing keys that are the same size as the plaintext is impractical. Therefore, other methods must be used to obscure ciphertext against frequency analysis in a simple substitution cipher. The impracticality of an 'infinite' key means that the randomness, or
entropy, of the encryption is introduced via the method.

We have seen the method of 'substitution'. Even in modern crypto, substitution is a valid technique. Another technique is 'transposition', or swapping of bytes.

Modern ciphers break into two types; symmetric and asymmetric.

Symmetric ciphers come in two flavours: block and stream.

Until now, we have been playing with classical ciphers, approximating 'block' ciphers. A block cipher is done in fixed size blocks (suprise!). For example, in the previous paragraphs we discussed breaking text and keys into 256 byte blocks, and working on those blocks. Block ciphers use a fixed key to perform substituion and transposition ciphers on each block discretely.

Its time to employ a stream cipher. A stream cipher attempts to create an on-the-fly 'random' keystream to encrypt the incoming plaintext one byte at a time. Typically, the 'random' key byte is xor'd with the plaintext to produce the ciphertext. If the random keystream can be replicated at the recieving end, then a further xor will produce the plaintext once again.

From this example forward, we will be working with bytes, not ASCII text, so a hex editor/dumper like hexdump is a necessity. Now is the right time to start to learn to use tools like cryptool.

In this example, the keyfile is in your directory, however it is not readable by you. The binary 'encrypt6' is also available.
It will read the keyfile and encrypt any message you desire, using the key AND a 'random' number. You get to perform a 'known ciphertext' attack by introducing plaintext of your choice. The challenge here is not simple, but the 'random' number generator is weak.

As stated, it is now that we suggest you begin to use public tools, like cryptool, to help in your analysis. You will most likely need a hint to get going. See 'HINT1' if you need a kicktstart.

If you have further difficulty, there is a hint in 'HINT2'.

The password for level 7 (krypton7) is encrypted with 'encrypt6'.

Good Luck!

This challenge will use a stream cipher. Furthermore, we’ll be able to do chosen-plaintext attacks using our input, plus a random number.

The first hint is as follows:

Let’s make a file in /tmp, and use Python to fill it with 50 As:

krypton6@krypton:/krypton/krypton6$ cd /tmp
krypton6@krypton:/tmp$ touch test.txt
krypton6@krypton:/tmp$ python -c "print 'A'*50" > test.txt

Then, link the keyfile, and run the encryption program:

krypton6@krypton:/tmp$ ln -s /krypton/krypton6/keyfile.dat 
krypton6@krypton:/tmp$ /krypton/krypton6/encrypt6 test.txt output.txt
krypton6@krypton:/tmp$ cat output.txt
EICTDGYIYZKTHNSIRFXYCPFUEOCKRNEICTDGYIYZKTHNSIRFXY

If we look at our output, we can see that it repeats after a certain number of characters:

EICTDGYIYZKTHNSIRFXYCPFUEOCKRN
EICTDGYIYZKTHNSIRFXY

Likewise, if we input a bunch of Bs into the input file, we get:

krypton6@krypton:/tmp$ python -c "print 'B'*50" > test2.txt
krypton6@krypton:/tmp$ /krypton/krypton6/encrypt6 test2.txt output.txt
krypton6@krypton:/tmp$ cat output.txt
FJDUEHZJZALUIOTJSGYZDQGVFPDLSOFJDUEHZJZALUIOTJSGY

Again, it repeats:

FJDUEHZJZALUIOTJSGYZDQGVFPDLSO
FJDUEHZJZALUIOTJSGY

These repeat after 30 characters. We now know that:

AAAAAAAAAAAAAAAAAAAAAAAAAAAAAA shifts to EICTDGYIYZKTHNSIRFXYCPFUEOCKRN
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBB shifts to FJDUEHZJZALUIOTJSGYZDQGVFPDLSO

With this in mind, given a shorter text like PNUKLYLWRQKGKBE, we can know the shift of each letter, then use that to remap the flag ciphertext.

A->E is a shift of 4 for the first letter, A->I is a shift of 8 for the second letter, and so on.

Here is a python script to automate this:

import string

cipher = "PNUKLYLWRQKGKBE"
cipherlength = len(cipher)

for i in range(0, cipherlength): 
    chosen = "AAAAAAAAAAAAAAA"
    encoded = "EICTDGYIYZKTHNS"
    print(ord(encoded[i]) - ord(chosen[i]))

# the above prints: 4, 8, 2, 19, 3, 6, 24, 8, 24, 25, 10, 19, 7, 13, 18

flag = ""
decode = [4, 8, 2, 19, 3, 6, 24, 8, 24, 25, 10, 19, 7, 13, 18]

for i in range(0, cipherlength): 
    char = ord(cipher[i]) # get the ciphertext character
    result = char - decode[i] # subtract to decode
    if (chr(result) not in string.ascii_letters): 
        result = char - decode[i] + 26

    flag += chr(result)

print(flag)

The answer is LFSRISNOTRANDOM.